This is probably an easy one for y'all but I seem to have replaced all the math storage in my brain with obscure facts about Yugos.
If you have a shape like the one below how do you determine the degee of taper on the sides?
This is probably an easy one for y'all but I seem to have replaced all the math storage in my brain with obscure facts about Yugos.
If you have a shape like the one below how do you determine the degee of taper on the sides?
(Bottom diameter-top diameter)/2 = bottom of a right triangle. Height = left side. After that, the angle of the slope upwards from the bottom will be inverse tangent of [the height (left side, Opposite) divided by the bottom of the triangle (Adjacent) ].
Throw us some numbers.
diameter of the top - diameter of the bottom / 2 = x height = y
then just use trig..
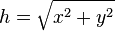
then sin=o/h cos=a/h tan=o/a
Dr. Hess wrote: (Bottom diameter-top diameter)/2 = bottom of a right triangle. Height = left side. After that, the angle of the slope upwards from the bottom will be inverse tangent of [the height (left side, Opposite) divided by the bottom of the triangle (Adjacent) ]. Throw us some numbers.
I'd throw you the numbers but the part isnt here with me so I have to measure when I get home.
Im trying to find out the required taper for a tie rod end based on the hole in the steering arm.
Yeah - measure it. It's not hard. If you can't measure it directly for some reason, treat it as a silhouette - measure the top and bottom diameters, measure the length, whip out some trip and whammo - angle is found.
I am guessing tie rod end into spindle... Dill them both out and use a stepped rod into a heim end ;)
You could look it up in the book of tie rod ends at the auto parts store. I think it's a Moog book. Anyone find the online version? There's only like 2 tapers used, and most are one.
John Brown wrote: I am guessing tie rod end into spindle... Dill them both out and use a stepped rod into a heim end ;)
Essentially what Im trying to do :) The heim adapter comes in 7 or 10 degree so I was trying to determine if either of those were close enough to just attack it with a reamer rather than drill out the whole spindle.
All I've found is the tapered ones, although I know the stepped ones, straight through, exist because I've seen them in projects but I cant seem to find a supplier, anyone have a source?
Anyone ever drilled these out before? How hard is is going to be with a cheap drill press?
Dr. Hess wrote: You could look it up in the book of tie rod ends at the auto parts store. I think it's a Moog book. Anyone find the online version? There's only like 2 tapers used, and most are one.
Yeah, I was looking for a reference source online but so far nothing.
Really there's only the 2? (7 and 10 Im assuming) that narrows it down. I thought there would be a greater variety.
Gearheadotaku wrote: Math is never simple...
Proof that 1 + 1 = 2
The proof starts from the Peano Postulates, which define the natural numbers N. N is the smallest set satisfying these postulates:
P1. 1 is in N. P2. If x is in N, then its "successor" x' is in N. P3. There is no x such that x' = 1. P4. If x isn't 1, then there is a y in N such that y' = x. P5. If S is a subset of N, 1 is in S, and the implication (x in S => x' in S) holds, then S = N.
Then you have to define addition recursively: Def: Let a and b be in N. If b = 1, then define a + b = a' (using P1 and P2). If b isn't 1, then let c' = b, with c in N (using P4), and define a + b = (a + c)'.
Then you have to define 2: Def: 2 = 1'
2 is in N by P1, P2, and the definition of 2.
Theorem: 1 + 1 = 2
Proof: Use the first part of the definition of + with a = b = 1. Then 1 + 1 = 1' = 2 Q.E.D.
Note: There is an alternate formulation of the Peano Postulates which replaces 1 with 0 in P1, P3, P4, and P5. Then you have to change the definition of addition to this: Def: Let a and b be in N. If b = 0, then define a + b = a. If b isn't 0, then let c' = b, with c in N, and define a + b = (a + c)'.
You also have to define 1 = 0', and 2 = 1'. Then the proof of the Theorem above is a little different:
Proof: Use the second part of the definition of + first: 1 + 1 = (1 + 0)' Now use the first part of the definition of + on the sum in parentheses: 1 + 1 = (1)' = 1' = 2 Q.E.D.
You'll need to log in to post.