mke said:
In reply to GTXVette :
When I raced bikes we used play pretty close attention to cold pressure vs hot pressure and temp rise to think we knew what pressure to set when....not sure I ever actually got it right like I knew real teams did but I always felt like I was being a serious racer :)
It was an Um Educated Guess UNTIL Da Dah Pressure bleeders came along, Dude On One Car (A Lefthander Chassis) we Would drop Start Pressure to 12 lbs inside rear, (We Didn't tell Gary) and it would still be blowing air after a 25 0r longer race

Ognib
New Reader
3/2/19 5:59 p.m.
Interesting conversation. Of interest to me as I'll eventually be dealing with these questions in my mini sprint build.
Just thought, spring frequency happens every 12 months.
I'll leave now.

mke
Dork
3/24/21 2:42 p.m.
I finally bought some springs.
Here's where the car is with the new front springs....1.49 front, 1.42 rear.

the ref I found is:
passenger car: 1.0
sports car 1.25-1.75
low/no down force autoX, roadrace 2.0-2.5
stock subaru brz 1.45 so my new SUPER stiff springs are nothing like super stiff and are actually what would be considered a soft spring, stiff bar setup I guess.
To get to 2.0Hz would be 1100/900....that's a lot of spring compared to what I here people are running on these cars! Another way I've done the math is 4" travel is good, and should have 1.5" sag max with 0 preload, that pops out 715/595 and says my new front spring belong on the back and I need new new front springs. The other end is 1" sag min with 0 preload pops out 1073/894 which matches the 2.0hz numbers...funny how the numbers all match up :)

mke
Dork
3/25/21 8:37 a.m.
I had an error in my spring spread sheet and the springs I ordered are kind of stiff and mismatched :( This goes back to page one where I said the online calculator didn't match the eibach math, the eibach math is right I'm pretty sure and I THINK I'm sort of getting this now.
I've always used a simple math based on sag...and it mostly works out, but I guess the idea with frequency is that you kind of want the car to stay level and for that to happen the f/r frequencies kind need to be the same. My sag math I think gets the car sitting right and the f/r roll stiffness kind of matched but probably isn't as good.....better to match up the frequencies then use sway bars to tune roll stiffness. That's what I'm understanding now anyway, not saying its right.
It looks like the 900 front should pair with 575 rears and yield 2.6hz which is kind or moving into downforce car territory.....but still softer than the simple sag math suggests I want. I generally prefer stiffer springs and small swaybars because roads here tend to be all patches on the right and a light bar lets just the right wheels bounce around and deal with it better....on smoother roads I suspect I'd prefer less spring and more bar....don't know but I'm going to let this order roll I think.
A buddy out has 580/380 and that is 2.1....so kind of the other end of the autocross/track range spring wise with 1"/.875" sway bars and says its good. With the heavier springs I'm going to stay where I am swaybar wise, 3/4 front, nothing rear and see....I suspect it will want a bit more front bar....but I need a running engine to be sure.

I

Driven5
UltraDork
3/25/21 9:38 a.m.
Can you show your work for the 'sag' math you're using? If as expected, it should be able to be used directly to calculate the natural frequency, and conversely it can be calculated directly from natural frequency.
Also, the F/R frequencies are generally not put too close together, as this tends to exaggerate the pitchiness of the car over bumps. Rear a bit higher than front, or front a bit higher than rear. While I tend toward higher rear than front frequencies, big spring small bar track cars especially do tend to be biased toward a higher front frquency. I believe this is basically the result of a rear frequency bias typically requiring a larger front bar to balance the car out. So perhaps consider dropping your rear rate a bit?

Frequencies have their place. Its best place is in the initial design/build phase to get you on the map. As soon as the tires hit the track you get to feel what the car needs and tune it to suit the driver and to suit the specific track and conditions, so you pretty much throw it out at that point while keeping it as something of a rough baseline. Its good for getting an idea of how much spring rates should vary front to rear and as a measuring stick of what your changes should mean to balance and to levelset expectations as far as bumps upsetting the car and not asking dampers to do a springs job (like pretty much every street class autocross car in existence winds up doing because of the rules - Artificially stiffening the car via dampers).
As far as calculating them, I have the Milliken textbook and tend to do my own spreadsheets or at least verify one I find isnt doing something funky (I have found several that I swear someone intentionally put errors into to screw up competitors).
I have been thinking about doing some work in regards to figuring out calculating wheel rates for my F500, but the whole testing to figure out the dynamic "spring rate" of the rubber puck canisters gives me pause, especially when I have a setup on the car that seems to be working. I am probably just going to work on computing motion ratios for each configuration of the pushrods and go from there having a +/- understanding of what changes mean and leave it at that.

mke
Dork
3/25/21 10:10 a.m.
In reply to Driven5 :
Its dead simple.....I say sag, the amount the car drops from tire just touching to give it a bounce and see where it settles should be about 1/3 of designed travel when preload is set to 0. Then 4" of travel is enough so 1.33" sag is the number. at the softer end would be 6" travel and 2"sag.
then I guess its just:
motion ratio (MR)= shock travel/wheel travel so
shock travel is desired Sag* MR
Required spring force = spung weight/MR
Spring rate = required force/shock travel
....I think that's right.

Driven5
UltraDork
3/25/21 12:07 p.m.
I'm glad I asked. You take a different path to the same point. It's an interesting methodology and mindset. But just know that they can be directly related, so whichever you understand easier can accomplish the same goal.
Wheel Travel = 9.818 / (Frequency^2)
Frequency = SQRT (9.818 / Wheel travel)
So roughly speaking:
1.5 Hz = 4.36"
1.75 Hz = 3.21"
2Hz = 2.45"
2.25 Hz = 1.94"
2.5 Hz = 1.57"
.
I will also say that I've seen and heard the 1/3 droop (sag) vs 2/3 bump thrown around a lot over the years for determining shocks. Notice the non-linearity of the above numbers. As best I can figure, it was probably said once in regards to a fairly specific type of application, and then others took the ball and ran (the wrong direction) with it by trying to apply it more universally. I disagree with it entirely as a widespread baseline, as any validity it has will only hold up within the narrow range of (unknown?) originally intended usage. Otherwise a stock Miata actually needs 19.5 inches of shock travel, 6.5" droop and 13" of bump... Which doesn't even come close to passing the 'sniff' test for me. 

mke
Dork
3/25/21 1:42 p.m.
I know where I got it from...motorcycle road racing and I've used it on a few car and been happy with the results. Its just about being stiff enough to stay off the snubbers in normal use and not so stiff it chatters.
I'm confused about your miata example.....the travel is a given at 4" for firm, 6" for soft, that never changes so it can't be 21". Then the droop/sag is always ends up 1.33-2" so by your Hz to inch calc the setup is always 2.25-2.5 hz? That seems a fine number to race a miata?.... but let me ask, what is the wheel travel formula? Those number don't quite match what my spread sheet is kicking out on my setup but I still may have something wrong somewhere.
Using the Eibach math I'm calculating 2.6hz F/R but with my math sag is 1.9" front and 1.5" rear....that is what has me a bit concerned as I'm pretty sure it means the rear roll stiffness is higher than the front and that probably means oversteer. and neither quite matches what you have which brings me back to not sure I understand what your wheel travel formula is outputing exactly?

mke
Dork
3/25/21 2:31 p.m.
mke said:
Using the Eibach math I'm calculating 2.6hz F/R but with my math sag is 1.9" front and 1.5" rear....that is what has me a bit concerned as I'm pretty sure it means the rear roll stiffness is higher than the front and that probably means oversteer. and neither quite matches what you have which brings me back to not sure I understand what your wheel travel formula is outputing exactly?
I found I'd made an error on the way I calculated droop.....I now get very close to your numbers and my F/R issue was how I was treating the angle.
Is the 9.818 gravity?

Driven5
UltraDork
3/25/21 3:19 p.m.
mke said:
I'm confused about your miata example.....the travel is a given at 4" for firm, 6" for soft, that never changes so it can't be 21". Then the droop/sag is always ends up 1.33-2" so by your Hz to inch calc the setup is always 2.25-2.5 hz? That seems a fine number to race a miata?
I'm not talking about a race Miata though... I'm talking about a stock Miata. If that generalization was even in the ballpark of widely applicable, it wouldn't spit out absolutely ridiculous shock travel requirements at normal sports-cars ride frequencies. For example, a stock Miata that I'm guessing is in the neighborhood of 1.23Hz. In order to get to a frequency that low with the 1/3 : 2/3 assumption, you'd have to have shocks and functionally available wheel travel that are both unrealistically and excessively disproportionate to reality.
And correction, I meant 6.5 + (2 * 6.5) = 19.5.
The thing is, that 1/3 : 2/3 assumption also doesn't specify what the ratio of that shock travel the bump stop should / would / could occupy. From the data I've seen, nothing has indicated to me that any more shock travel is necessary (for non-aero road/track applications avoiding bump stop interaction) than (sag*2)+bump stop... And if that does indeed work out to 1/3 : 2/3, it's more of a happy coincidence of happening to fall within a similar range of applications than it is by actual design IMHO. So if that's the only application of ever design for, it probably works well enough, but has loads of room for improvement. Honestly though, I believe that is still rather conservative for most applications, as it allows for more free bump travel than most any car seems to actually use in practice. I have long wanted to put this to the test. My intuition is that closer to (sag*1.75)+bump stop, or even (sag*1.5)+bump stop, would likely still be plenty adequate for most applications.
No, 9.818 is actually not gravity. If you go back to the Eibach formulas from page 1, you'll see 187.8 referenced in addition to 60 for the cpm to Hz conversion. I guess I'm off a little too though, as I rounded to 188. 9.818 = (188/60)^2. Apparently the 9.797 (from using 187.8) would be a little more accurate. To get to where the 188 (187.8) comes from I'd have to dive back into the derivation of the formulas, which I haven't done in years.

mke
Dork
3/25/21 3:56 p.m.
The "rule"...aka rough guideline is for roadracing, nothing to do with a stock anything, no sense optimizing parts you're going to throw out ;) As I said the travel is given, not calculated and is 4-6", so sag is always 1.33-2"...and we now know that results is saying 2.2-2.7Hz is good. That seems not so bad but a little stiffer than the 2-2.5 I see as a good roadrace setup baseline range.
Its from roadracing motorcylces which have a pretty high GC and a lot of F/R motion during accel/decel, literally the front is off the ground on accel and rear off the ground on braking but for sure with cars that is not the case so I guess cars can be a bit softer without riding on the snubber issues......I'd have to think about a new rule....maybe 1/2 the travel in sag and assume travel at 3-5" would about work out? I seem to recall someone suggesting 1/2 to me at one point so it might already be someone elses rule :) Doesn't matter I guess.

BA5
Reader
3/25/21 5:03 p.m.
GameboyRMH said:
Unless you're very serious about performance suspension tuning it's not worth caring about. I've done more detailed suspension tuning than most and I don't have much use for the number - its function seems to be just a numerical evaluation of the effective stiffness of a car's suspension. Good for comparing cars perhaps, not so useful for tuning an individual car, at least in this hobbyist's experience.
When calculating the number it's very easy for the calculations to be greatly thrown off by incorrect inputs.
Edit: BTW, I'm assuming you're talking about what's more commonly referred to as suspension frequency or wheel frequency. You need unsprung weights and corner weights to calculate it.
I generally agree with sentiment with one caveat: I wound up with a setup at one point that had my front/rear pretty out of sync and the car would pitch in heave weird ways. I re-sprung the rear based off of the front ride frequency so that it would 'catch up'. I was pretty happy with the results and thought it made a pretty marked improvement in the car's drivability.

mke
Dork
3/26/21 7:49 a.m.
mke said:
As I said the travel is given, not calculated and is 4-6", so sag is always 1.33-2"...and we now know that results is saying 2.2-2.7Hz is good.
Driving to the office this morning I realized I just love over complicating stuff.....travel and % travel really has nothing to do with it ....its 1.5-2.5" sag puts you in the sweet spot for autoX and roadracing without doing or thinking about any math :)

Driven5
UltraDork
3/26/21 8:37 a.m.
In reply to mke :
Exactly. It doesn't really matter if you have 6" of available travel or 16" of available travel, you're still generally looking at rates that will put you in the 1.5"-2.5" sag range.
The travel and travel % is more about component selection and setup, to ensure that there is enough travel to not hit the bump stops during normal operation, but ideally not so much that the spring, control arm, tire, or chassis runs out of range of motion... In other words: You want the bump stop to primarily be what stops the bump motion. As long as the spring, control arms , tires, and chassis all have the available range of motion to run 1/3 : 2/3 (or more) at the desired ride height, there no real harm in doing so. But regardless of whether the car is stock or purpose built for racing, this is often not a realistic possibility.

nocones
UberDork
3/26/21 11:24 a.m.
I made this for my build thread but thought I'd drop it here also. What's interesting about it is how below ~2.0 Hz, the WR/Sprung mass ratio can be radically different with relatively minor impacts to frequency. From 2-3 hz, it's relatively linear as SAG drops from ~2.0" to 1.0". At 3 Hz things start to get aggressive for the impacts to Frequency for relatively small impacts to springrate changes. I mean that's just how ^2 functions are but the way the function lays over different types of cars is interesting.
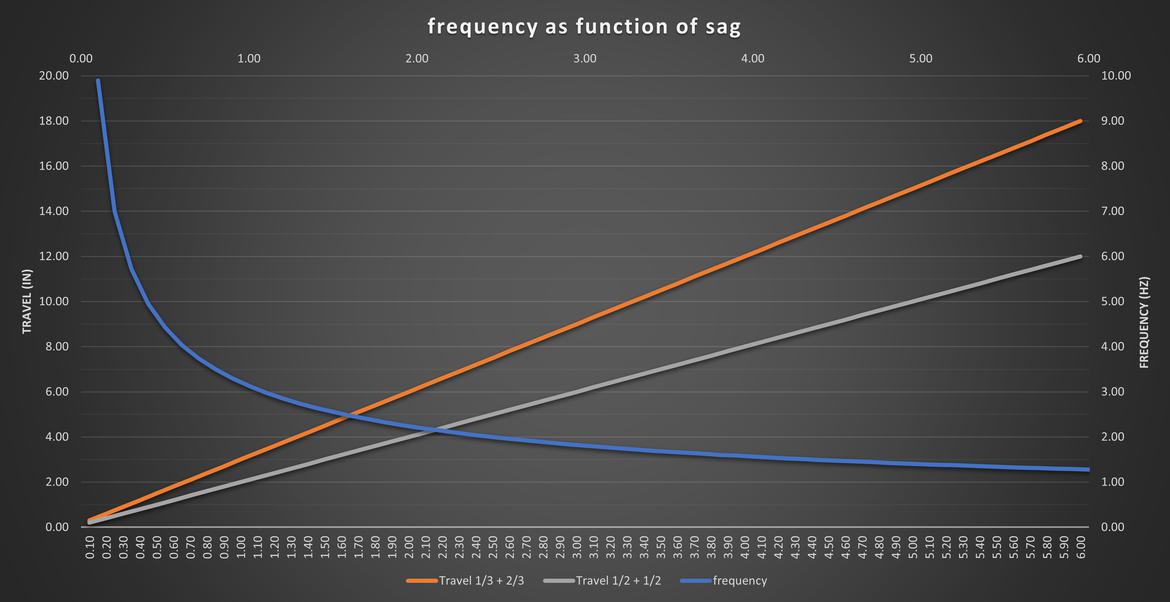
It's just a plot of natural frequency as a function of SAG. I've included total travel lines of 1/2 Sag + 1/2 bump, and 1/3 Sag + 2/3 bump. My MG is closer to 1/2+1/2 then 1/3+2/3. That said I'm not sure how progressive the bellcranks end up being. They should be fairly linear but they do inherently get progressive because the shock lever arm is longer then the pushrod lever arm on both Front and rear suspensions. This makes them inherently some amount progressive, but the rears are close to 1.1:1 and angualar rotation is fairly low because the total shock travel is short (2") on the sportbike shocks I'm using.

mke
Dork
3/27/21 6:48 a.m.
I like it! Somehow I missed your build thread, I have some catching up to do.

Bump for personal benefit -
How about a lightweight rear engine car?
Or, what role does weight distribution play? As a lot of you know, I'm building a V6-swapped Lotus Europa. The car will maintain its stock front suspension, but I am designing a SLA rear suspension. There are spring upgrades for the front, but front motion ratio will not change. The original Lotus weighed 1500 lbs, 45/55 front-rear distribution, and seemed to be designed for a 0.95 to 1.0 Hz ride frequency based on my reverse-engineering. Stock front springs are 100 lbs/in.
New weight will be 2000 to 2200 lbs, 40/60% or maybe even 35/65% front-rear. I have some 525 lb/in sport bike shocks for the rear, and from initial geometry/MR's etc, it's looking like 0.90 Hz front and 1.40 Hz rear. What do we think of this as a ball park for a street-driven fun car/$2000 Challenge autocrosser?
For comparison, the McLaren F1 is 42/58 front-rear with frequencies of 1.43 Hz front and 1.80 Hz rear. I can upgrade front springs and get the front frequency up to 1.20 or even 1.40. Rear MR does not have much adjustment due to packaging unless I go full rocker arms.
Frequency is nice because it takes into account sprung weight. You could call it rate/lb and get a different number but the same idea.

mke
Dork
12/20/21 2:27 p.m.
if you can get the front up to 1.4 to match the rear, I would as 0.9 hz more old Cadillac than autocross. As Pete says, the whole idea of spring freq is it it takes the weight and and ratio into account so you can compare different setups more directly. When you see a mismatch like the McLaren I would assume that is due to the aero package effectively adding weight in the rear.
In reply to mke :
Roll centers and sway bar rates also screw with it as far as cornering is concerned.
I always figured that frequency gets you in the ballpark as far as pitch control is concerned (which is why they tend to be lower in the front) and then handling gets controlled with sway bars dependent on roll center height (which is why cars tend to have big front bars).
And then you drive it and say "this is all wrong!" but at least you had a decent place to start your first approximation...
I'm with Pete, found it useful to ballpark a new car to get started and have a place to work from. That said, generally changes to be made for driver preference, surfaces raced, tire reaction, etc.
Use it before first test, then use it to educate change magnitudes