RevRico
MegaDork
11/8/24 11:50 a.m.
I was going to just ask my father in law, the long tenured CMU mathematician, but that would only be one point of view. Here there's all kinda of engineers, statisticians, I think some chemists, maybe you've encountered this stuff.
We're all familiar with exponents, yes? Little number on the top right of the big number that tells you how many times to multiply the big number by itself.
Well last night I learned the little number can go top left, and create tertration, which is basically (extreme paraphrase) an exponents exponent.
Well this continues into pentation and hexation in the bottom left and right respectively.
The thing is, these are ridiculously large numbers. Like, there are more digits in the number than there are atoms in the universe kind of enormous numbers.
And then there is a thing called a TREE function, which takes those already unimaginably huge numbers and multiplies them by themselves a crap load of times again.
Why? "Because we can" is an answer I'll accept, but I'm wondering if there is an actual use case for this sort of math. I could see maybe encryption, but I don't know what else could use such enormous numbers.
You're right, we don't need this for counting things but it's useful for counting possible interactions, events over time, etc..
Edit...
I don't believe I've ever seen this suggested but I've thought for a long time that using a decimal point in the exponent would work better than the counter-rotation exponent placement convention that we currently have.
Four (pun intended) example...4^2.2 = 256.
Those kinds of numbers are too big to even be relevant to cryptography in the foreseeable future, but in math practicality has never been a consideration and "because we can" is as good a reason as any.
Those numbers are the number of watts it will take to go warp 1
VolvoHeretic said:
Those numbers are the number of watts it will take to go warp 1
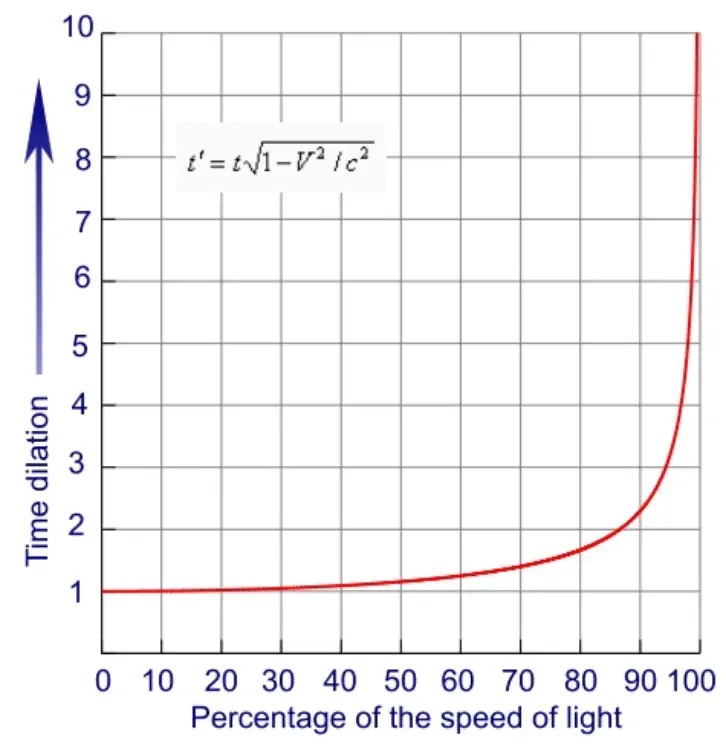
As I'm sure you know, we'll need fundamentally different principles to operate on.
I mean, currently, getting one bird's feather to 0.99 C would require the collective energy of multiple average sized stars.
I found one area of cryptography where such stupendously huge numbers are used, the product of the large primes used in public/private key cryptography can be hundreds of digits long in decimal (!) but being a product of oddball primes, tetration etc likely wouldn't be useful for representing them.
GameboyRMH said:
Those kinds of numbers are too big to even be relevant to cryptography in the foreseeable future, but in math practicality has never been a consideration and "because we can" is as good a reason as any.
I think they make good placeholders for equations where maybe you don't need THE big number, but you need to define some smaller number by its terms.
I am thinking in a way of numbers like i. That number doesn't exist. It cannot exist, that's why it's called imaginary. There is no way that the square of any number can equal a negative number, because a negative times a negative is a positive. But it's useful as a placeholder in an equation where it may be canceled out by an i on the other side and you end up with a real number.
GameboyRMH said:
I found one area of cryptography where such stupendously huge numbers are used, the product of the large primes used in public/private key cryptography can be hundreds of digits long in decimal (!) but being a product of oddball primes, tetration etc likely wouldn't be useful for representing them.
A lot of primes are squares minus two.
Two squared minus two is prime. Three squared minus two is prime. Five squared minus two is prime, seven squared minus two is prime, nine squared minus two is prime...
I don't know about the fancy pants other factors though 

ShawnG
MegaDork
11/8/24 8:47 p.m.
That's the math Russia is using to calculate the interest on the fines that Google owes.

cyow5
Reader
11/8/24 9:19 p.m.
RX Reven' said:
You're right, we don't need this for counting things but it's useful for counting possible interactions, events over time, etc..
Edit...
I don't believe I've ever seen this suggested but I've thought for a long time that using a decimal point in the exponent would work better than the counter-rotation exponent placement convention that we currently have.
Four (pun intended) example...4^2.2 = 256.
But 4^2.2 already has a useful meaning (21.1) and encoding the decimal point would create ambiguity

cyow5
Reader
11/8/24 9:19 p.m.
RX Reven' said:
You're right, we don't need this for counting things but it's useful for counting possible interactions, events over time, etc..
Edit...
I don't believe I've ever seen this suggested but I've thought for a long time that using a decimal point in the exponent would work better than the counter-rotation exponent placement convention that we currently have.
Four (pun intended) example...4^2.2 = 256.
But 4^2.2 already has a useful meaning (21.1) and encoding the decimal point would create ambiguity